CONTENTS:
-DISCUSSION
-ANALYSIS
OF DIAGRAM AND
GRAPHING PRESENTATION
-CONVERTION
-FORMULAS
-COMPARE AND CONTRAST
-IMPORTANT POINTS
-LEARNINGS (Technical and
Nontechnical)
“When wireless is fully applied the earth will be converted
into a huge brain, capable of response in every one of its parts.”
-----Nikola Tesla------
Everytime we see a
sinusoidal waves, an idea is directly formulated into our minds that it is an
alternating current (ac) in which the voltage and current are varying. We may
also differentiate direct current (dc) and alternating current (ac) through its
frequency. For short history of dc and ac sources, at the end of 19th
century, these two were hotly debated. Thomas Edison leads the dc source side
while Nikola Tesla leads the ac source side. Until 1800’s, dc sources serves as
the main means of providing electric power but, after this century, another
battle began between the said sources. Since alternating current is more
efficient and economical especially easy to generate and transmit long
distances, it ended up as the winner.
WHAT IS ALTERNATING CURRENT??
Alternating Current serves
as the primary mode of electricity transmission and distribution.
In the
circuit diagram of a power supply, before entering the bridge, it is still
alternating current but, after it goes through the bridge, it is already a
direct current. In terms of the sinusoidal wave of an alternating current, appliances
in our house are an example such as electric fan. Each of it’s blades have
different waves. It may start to generate at different voltage but have the
same peak or maximum voltage.
Sinusoid is a signal that has the form of sine and cosine
function.
v(t)=Vm
cos (ɷ t+ᶲ)
where:
Vm=
amplitude of sinusoid
ɷ=
angular frequency in rad/s
formula:
ɷ=2πf
ᶲ=
phase
We may also experience sinusoidal variation in:
Period is the time of one complete cycle or the number of
seconds per cycle.
Frequency is the
rate at which something occurs over a particular period of time.
NOTE:
Horizontal
axis= magnitude of cosine
Vertical
axis= magnitude of sine
Clockwise
direction= measures negative from horizontal axis
Counterclockwise=
measures positive from horizontal axis
OUT OF PHASE
IN PHASE
When ᶲ≠0 or v1 and
v2 do not have the same angle, it is said to be out of the phase. When
ᶲ=0 or v1 and v2 have the same angle, it is said to be in
phase. Both situations don’t consider the amplitude or the peak voltage.
Lagging= the greater angle
with respect to horizontal axis
Leading= the smaller angle
with respect to horizontal axis
Phasor is a complex number
that represents the amplitude and phase of sinusoid. It is the easier way to
express sinusoids. It is also convenient to use with the sine and cosine
function but, before we apply phasors in circuit analysis, we need to
completely engaged and familiar with complex numbers.
Complex numbers may be in the form of:
Rectangular form: z=x+jy
Polar form: z=r< ᶿ
CONVERTION:
NOTE:
We can
only subtract and add complex numbers in rectangular form. Just add or subtract
the real part and imaginary part. When we divide and multiply, it must be in polar
form. In division, just divide the radius and subtract the angles considering
its sign convention. In multiplication, just multiply the radius and add the
angles.
TIME DOMAIN
-v(t)=Vm cos (ɷ t+ᶲ)
-time dependent
-always real with no
complex term
PHASOR DOMAIN
-V= Vm
< ᶿ
-time independent
-generally complex
NOTE:
To
get phasor corresponding to sinusoid, first express the sinusoid in the cosine form
so that the sinusoid can be written as the real part of a complex number.
IMPEDANCE AND ADMITTANCE
3 Basic Formulas:
where:
Y= admittance measured in siemens
form: Y=G+jB
RESSITOR ------------------------------------- ᶿI is
equal to ᶿV
INDUCTOR
------------------------------------- ᶿI
is
less than ᶿV
CAPACITOR ------------------------------------- ᶿI is
greater than ᶿV
Inductor
is a short circuit in dc source but at high frequency, it is an open circuit.
Capacitor is an open circuit at dc source but short circuit at high frequency.
Since ɷ=2πf, the angular frequency increases as frequency (f) increases.
For actual application,
consider the two ac circuit below with the same degree and frequency and
different voltage.
WHAT WILL BE THE RESULTING WAVE??

NOTE:
The result
above was gathered during the conduction of our experiment about the
characteristics of sinusoid. The wave was graphed using the oscilloscope.
Generally, I’ve
learned that when the time the v1 and v2 moves upward is
the same, is phasor difference is zero since the time difference is also zero. I’ve
also learned that it is nice to the feeling that a certain idea discussed in
the book or internet will be proven using actual applications in the form of
experiment. Now I completely realized that analyzing a certain circuit is not that easy especially if the given parameters are not just a real number but a complex one.








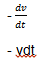




Walang komento:
Mag-post ng isang Komento