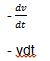∫! nU∫ɸ!DaL ∫Ʈ€aDy- ∫t aƮ€ aNaLy∫! ∫

N ɸ d a [  a N a [ y ∫ ǃ∫

NODE- meeting point of branches

            The basis of nodal analysis is Kirchhoff’s Current Law. We can analyze AC circuits by nodal analysis since KCL is valid for phasors. As what we had discussed in Circuits 1, nodal analysis provides a general procedure for analyzing circuits using node voltages as the circuit variables. By choosing node voltages instead of element voltages as circuit variables, it reduces the number of equations one must solve. In getting nodal equations, we must apply the various steps and rules we've been discussed in Circuits 1.

            There are also circuits containing supernode which a voltage source is connected between two non-reference nodes.

            If the circuit is not yet in its frequency domain, we must first convert the circuit such as the given example below.

Tips on transforming network:

-Use only magnitude and phase angle in transforming sources into phasors.

-Transform inductors by converting L to jωL.

-Transform capacitors by converting C to 1/jωC. Note that the units are in ohms.

-Resistors do not require transformation.

-Transform unknown functions of time through writing them as general phasors.

For further understanding of NODAL analysis, see sample problem below on how to formulate equations.

 

FORMULATED EQUATION:

      

            I've learned that Nodal analysis is efficient when there are fewer node equations than mesh equations. Applying Nodal analysis is slight difficult to use more especially if we’re dealing with complicated circuits. We can use this method if we are asked to solve for the voltage across a certain element or simply the node voltages. KCL is mainly the essential component of Nodal analysis which requires knowing the current through each element.

p H α ∫ ∈ - ∫ h ! f +∋ R ∫

Phase shifting is used to correct an undesirable phase shift that is already in the circuit or to produce special effects. RC, RL and any reactive circuit are very much suitable with this purpose or function in the sense that the capacitor makes the current lead the applied voltage.

For further understanding of phase- shifters, see sample problem below in a given two RC circuit. Compare and contrast their output voltage and their phase angle.

Use Voltage Division:

              

                             

We can say there were a lot of practical applications of phase shifting. Sound may be interpreted through phase shift. Shifting a specific radio station to other is an example of phase shifting. When we have two points of sound, there will be a time delay between those points that would cause phase shifting between the two waves.

I've learned that the phase of sinusoidal wave may also be shifted depending on the value of resistor (R), capacitor (C), and the operating frequency (f). I found out that when the output voltage (V_O), is taken across the resistor, phase angle is positive which made V_O leads the input voltage (V_i ) but, if V_O  is taken across the capacitor, V_O  lags V_in  a certain angle. Also, the total phase shift is equal to the sum of individual phase shifts.

αLτєRnατ!nG cµrRєNτ

CONTENTS:

            -DISCUSSION

            -ANALYSIS OF DIAGRAM AND

 GRAPHING PRESENTATION

-CONVERTION

-FORMULAS

-COMPARE AND CONTRAST

-IMPORTANT POINTS

-LEARNINGS (Technical and Nontechnical)

“When wireless is fully applied the earth will be converted into a huge brain, capable of response in every one of its parts.”

                                                                        -----Nikola Tesla------

Everytime we see a sinusoidal waves, an idea is directly formulated into our minds that it is an alternating current (ac) in which the voltage and current are varying. We may also differentiate direct current (dc) and alternating current (ac) through its frequency. For short history of dc and ac sources, at the end of 19^th century, these two were hotly debated. Thomas Edison leads the dc source side while Nikola Tesla leads the ac source side. Until 1800’s, dc sources serves as the main means of providing electric power but, after this century, another battle began between the said sources. Since alternating current is more efficient and economical especially easy to generate and transmit long distances, it ended up as the winner.

WHAT IS ALTERNATING CURRENT??

Alternating Current serves as the primary mode of electricity transmission and distribution.

          

            In the circuit diagram of a power supply, before entering the bridge, it is still alternating current but, after it goes through the bridge, it is already a direct current. In terms of the sinusoidal wave of an alternating current, appliances in our house are an example such as electric fan. Each of it’s blades have different waves. It may start to generate at different voltage but have the same peak or maximum voltage.

Sinusoid is a signal that has the form of sine and cosine function.

            v(t)=V_m cos (ɷ t+ᶲ)    

where:

            V_m= amplitude of sinusoid

            ɷ= angular frequency in rad/s

                        formula: ɷ=2πf

            ᶲ= phase

We may also experience sinusoidal variation in:

       

          a.)motion of pendulum  

    

          (b.) vibration of string

Period is the time of one complete cycle or the number of seconds per cycle.

Frequency is the rate at which something occurs over a particular period of time.

                    

 

NOTE:

            Horizontal axis= magnitude of cosine

            Vertical axis= magnitude of sine

            Clockwise direction= measures negative from horizontal axis

            Counterclockwise= measures positive from horizontal axis

            

 

                       OUT OF PHASE

                          IN PHASE

When ᶲ≠0 or v₁ and v₂ do not have the same angle, it is said to be out of the phase. When ᶲ=0 or v₁ and v₂ have the same angle, it is said to be in phase. Both situations don’t consider the amplitude or the peak voltage.

Lagging= the greater angle with respect to horizontal axis

Leading= the smaller angle with respect to horizontal axis

Phasor is a complex number that represents the amplitude and phase of sinusoid. It is the easier way to express sinusoids. It is also convenient to use with the sine and cosine function but, before we apply phasors in circuit analysis, we need to completely engaged and familiar with complex numbers.

Complex numbers may be in the form of:

Rectangular form: z=x+jy       

Polar form: z=r< ᶿ

CONVERTION:

Rectangular - Polar

Polar – Rectangular

x= r cos ᶿ 

y= r sin  ᶿ 

NOTE:

            We can only subtract and add complex numbers in rectangular form. Just add or subtract the real part and imaginary part. When we divide and multiply, it must be in polar form. In division, just divide the radius and subtract the angles considering its sign convention. In multiplication, just multiply the radius and add the angles.

TIME DOMAIN

-v(t)=V_m cos (ɷ t+ᶲ)   

-time dependent

-always real with no

 complex term

PHASOR DOMAIN

-V= V_m < ᶿ

-time independent

-generally complex

NOTE:

To get phasor corresponding to sinusoid, first express the sinusoid in the cosine form so that the sinusoid can be written as the real part of a complex number.

IMPEDANCE AND ADMITTANCE

            3 Basic Formulas:

                            where:

                                                

                                                  Y= admittance measured in siemens

                                                  form: Y=G+jB

RESSITOR       -------------------------------------          ᶿ_I is equal to ᶿ_V

INDUCTOR    -------------------------------------           ᶿ_I is less than ᶿ_V

CAPACITOR -------------------------------------           ᶿ_I is greater than ᶿ_V

           

            Inductor is a short circuit in dc source but at high frequency, it is an open circuit. Capacitor is an open circuit at dc source but short circuit at high frequency. Since ɷ=2πf, the angular frequency increases as frequency (f) increases.

            For actual application, consider the two ac circuit below with the same degree and frequency and different voltage.

             

                

             The Channel A and Channel B probes of oscilloscope is connected across the 1KΩ resistor.

WHAT WILL BE THE RESULTING WAVE??

NOTE:

            The result above was gathered during the conduction of our experiment about the characteristics of sinusoid. The wave was graphed using the oscilloscope.

            Generally, I’ve learned that when the time the v₁ and v₂ moves upward is the same, is phasor difference is zero since the time difference is also zero. I’ve also learned that it is nice to the feeling that a certain idea discussed in the book or internet will be proven using actual applications in the form of experiment. Now I completely realized that analyzing a certain circuit is not that easy especially if the given parameters are not just a real number but a complex one.