Instantaneous and Average Power & Maximum Average Power Transfer

               Power is said to be the most important quantity in electric utilities, electronic and even communication systems because these systems involve transmission of power from one point to another. Using ac in power generation began after the successful contribution of Tesla. Ac allowed high voltage power transmission from different power generating plant to the consumers compared to dc.

INSTANTANEOUS POWER

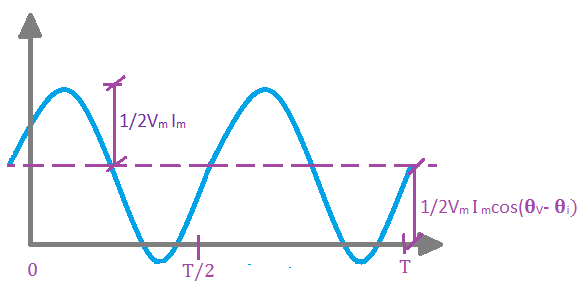
               Instantaneous power- the power absorbed by an element at any instant of time. It is just the product of instantaneous voltage v(t) across the element and the instantaneous current i(t) through it.

            

We noticed in the sketch of p (t) above that the power is positive at some part and negative for the rest of the cycle. This means that when:

p (t)>0: power is absorbed by the circuit

p(t)<0: power is absorbed by the source

The conditions stated above is possible to happen because of the presence of inductors and capacitors which are considered to be a storage elements. I conclude that power is transferred from the circuit to the source. Such as if a certain circuit has large voltage and current, the circuit has large power otherwise, less power. Power is directly proportional to the voltage and current. Thus, when voltage and current increases, power also increases.

AVERAGE POWER

               Average power- the average of instantaneous power over one period.

SAMPLE PROBLEM:

If v(t) = 160 cos 50t V and i(t) = –20 sin(50t – 30°) A, calculate the instantaneous power and the average power.

SOLUTION:

v(t) =160cos(50t)

i(t) = -20sin(50t −30°) = 2cos(50t −30°+180°−90°)

i(t) = 20cos(50t +60°) 

MAXIMUM AVERAGE POWER TRANSFER

               The maximum average power can be transferred to the load if X_L=-X_TH and R_L=R_TH. The load impedance Z_L must be equal to the complex conjugate of the Thevenin impedance Z_TH. We calculate V_TH and R_TH to get the maximum average power transfer.

SAMPLE PROBLEM:

 For real life application, we also have what we called power matching. For example, you bought an electronic appliance from other country then when you used it, it doesn't work. What would be the possible reasons why this happened? Maybe one of those reasons would be, the electric power in other country doesn't match to the electric power here in Philippines since we commonly used 50-60 Hz ac power. As we noticed, the electrical devices and appliances in our household such as electric fan, television, computer and etc. have its own power rating. This indicates how much power the equipment requires. Over power rating may lead to a permanent damage to the appliance.

Source Tranformation, Thevenin and Norton's Theorem

SOURCE TRANSFORMATION

Performing a source transformation consists of using Ohm’s Law. One can be derived from the other. This method can be performed on a circuit involving capacitors and inductors, as long as the circuit is first put into the frequency domain.

An ac voltage source V in series with an impedance Z can be replaced with an ac current source using this formula: (I=V/Z) connected in parallel with the impedance Z. An ac current source I in parallel with an impedance Z can be replaced with an ac voltage source of value using this formula:  (V=IZ) in series with the impedance Z.

TRANSFORMATION:

  

NOTE:

Using this method, we must keep these things in mind. First, apply Ohm's Law Second, impedances remain the same. Third, the arrow of the current source is directed toward the positive terminal of the voltage source.

I've learned that in source transformation, we used to get the equivalent circuit whose voltage-current characteristics are identical with the original circuit.  Also, dependent voltage source in series with impedance can be transformed to dependent current source in parallel with the impedance. For personal insights, source transformation is the easiest among the methods discussed because it is less confusing and you can easily understand it very well.

THEVENIN AND NORTON’S THEOREM

The application of Thevenin and Norton’s theorem to ac network is just the same as that outlined for dc networks. The only difference is that the quantities being used in dc are all real values while in ac are phasors and complex numbers. These theorems enable one to replace a complicated circuit with a simple equivalent circuit. These are used to isolate a portion of the circuit then the remaining portion of the circuit is transformed into an equivalent circuit.

THEVENIN’S THEOREM

This theorem has an equivalent circuit containing only a voltage source and a series connected impedance. The V_Th is also known as an open circuit voltage.

See figure below:

A Thevenin equivalent circuit is one that produces the same voltage and current to a given load as the original circuit that it replaces.

HOW TO CALCULATE THE THEVENIN EQUIVALENT CIRCUIT???

·       . Calculate Z_Th

Ø  Set all sources to zero or simply replace voltage sources by short circuits and current sources by open circuits.

Ø  Then find the total impedance between the two terminals.

·       Calculate V_Th.

Ø  Find the open circuit voltage between the terminals. 

NOTE:

Don’t deadened dependent sources because they are controlled by circuit variables.

NORTON’S THEOREM

               This theorem has an equivalent circuit containing a current source and a parallel connected impedance. The I_N is also known as a short circuit current.

See figure below: 

          The current source in Norton equivalent circuit is usually dependent on the electric signals applied to the input terminals.
 
HOW TO CALCULATE THE NORTON EQUIVALENT CIRCUIT???

·       . Calculate Z_N

Ø  Set all sources to zero or simply replace voltage sources by short circuits and current sources by open circuits.

Ø  Then find the total impedance between the two terminals.

·       Calculate I_N. 

Ø  Find the short circuit current between the terminals. 

          Through the discussions in our class and the informations I've read, I've learned that Norton’s theorem is just the derivation of the Thevenin’s theorem. They both have equal magnitude of impedance and also, their equivalent circuit can easily be interchanged by just applying Ohm’s Law. Most importantly, these theorems provide a method of reducing a more complex circuit to a simpler one and more manageable form for analysis. Lastly,I've learned that these theorems are very important from both theoritical and practical viewpoints since it is useful in calculating and simulating changes for large scale circuits.

SUPERPOSITION THEOREM

WHAT IS THE PRINCIPLE OF SUPERPOSITION?

            The principle of superposition states that the voltage across or the current through an element in a linear circuit is the algebraic sum of the voltages or the current through that element due to each independent source acting alone.

            There’s a lot of theorems we’ve been discussed in Circuits 1 and one of those is the superposition theorem in which it is not only applicable to dc circuit but also in an ac circuit. If a given circuit has two or more independent source, one way to determine the value the specific variable is to add up the contribution of each source.

IMPORTANT POINTS TO REMEMBER:

·         Superposition theorem cannot be applied if there’s only one source.

·         We only consider one independent source at a time.

·         Dependent source are left.

HOW TO APPLY SUPERPOSITION IN A GIVEN CIRCUIT?

·         Deadened all independent sources except one source. Then, determine the value of the required circuit variable.

·         Repeat first step in each other sources.

·         Add up the contributions of each independent source.

Voltage source (short circuit)

Current source (open circuit)

MAKE USE OF THE EXAMPLE BELOW:

           This problem is taken from the book of Alexander Sadiku

              (Fundamentals of Electric Circuits)

                                                FINAL ANSWER

            I’ve learned that in ac analysis using superposition theorem that we must add up the responses due to the individual frequencies in the time domain if the sources of the given circuit is operating at different frequencies. It is in the sense that the impedances depend on the frequency. I f a given circuit is composed of two ac sources with different frequencies and a dc source; the final answer would be in three terms. Note that in dc, capacitors act as an open circuit while inductors act as short circuit.

ɱ ϵ ∫ #  a Na [ y ∫ ǃ ∫

                

MESH- a loop which does not contain any other loop.

            Kirchhoff’s Voltage Law is the basis of mesh analysis. Like nodal analysis, mesh analysis is also used in analyzing AC circuits. It also provides another general procedure for analyzing circuits using mesh currents as the circuit variables. Using mesh currents as circuit variables is more convenient than using element currents because through this, it lessens the number of equations to be solved. Keep in mind that mesh analysis is only applicable to a planar circuit that’s why it is not that general as the nodal analysis.

            There are also circuits containing supermesh which doesn't have current of its own and two meshes shares in one current source.

            For further understanding of MESH analysis, see sample problem below on how to get equations from a given circuit.

                     EQUATION:

             I've learned that in mesh analysis, we must first assign mesh currents in a given circuit but it is also necessary to apply some strategies that could simplify the circuit to lessen the number of mesh currents and to come out in a few number of equations. There were also some circuits that fit the case 1 in which the current source existing only in one mesh is already the current of that mesh. For me, mesh analysis is convenient to use if current is unknown. If ever voltage is the unknown and we are asked to use mesh analysis. It is also easy to solved by just applying Ohm's Law.